수학, 더 이상 어렵지 않다! 정승재 강사가 알려주는 분수, 방정식, 농도 문제 개념 정리! 학생들이 자주 하는 실수를 바로잡고, 개념을 쉽게 이해하는 방법을 알려드립니다. 수포자 탈출을 원한다면 꼭 읽어보세요.

1. 분수 개념: 숫자가 아닌 ‘나눔’으로 이해하기
◎ 분수란?
정승재 강사는 분수를 단순한 숫자가 아니라 ‘나눗셈을 표현하는 방법’으로 설명한다.
☞ 예를 들어, 가래떡이 네 개 있을 때 이것을 4등분하면 4분의 1(¼) 이 된다.
이 개념을 이해하려면 다음을 기억해야 한다.
- 분자(위 숫자): 나누어진 개수
- 분모(아래 숫자): 전체를 나눈 개수
즉, 분수는 나눗셈 그 자체다.
📌 학생들이 흔히 하는 실수
● "4분의 1(¼)과 8분의 2(²/₈)는 다른 값이다"라고 생각하는 경우
● "분수는 그냥 계산하면 되는 숫자다"라고 외우는 경우
✅ 해결법: 분수는 비율과 나눗셈을 표현하는 방법이라는 것을 이해해야 한다.
피자로 이해하는 분수
피자가 8조각으로 나누어져 있을 때 한 조각은 8분의 1(⅛) 이다.
만약 두 조각을 먹었다면 8분의 2(²/₈) 라고 표현할 수 있다.
이처럼 분수는 단순한 숫자가 아니라 ‘나누어진 개수’라는 것을 확실히 이해해야 한다.

2. 분수의 기본 성질: 약분과 통분
① 약분: 분수를 간단하게 만드는 과정
✅ 약분 공식: 분자와 분모에 같은 숫자를 나누면 값이 변하지 않는다.
→ 8분의 4(⁴/₈) = 4분의 2(²/₄) = 2분의 1(½)
📌 학생들이 흔히 하는 실수
● 분수를 약분할 때 "그냥 외운 대로 한다"
● 약분할 때 분모와 분자에 다른 숫자를 나눔
✅ 해결법: 분자와 분모에 같은 숫자를 나눠야 한다는 개념을 먼저 이해해야 한다.
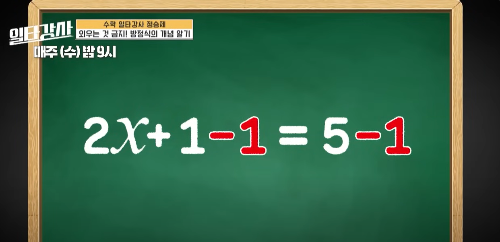
② 통분: 다른 분모를 가진 분수를 맞추는 과정
✅ 분모가 다를 경우, 같은 분모로 바꿔야 한다.
예제 1: 4분의 1(¼) + 8분의 1(⅛) = ?
- 4분의 1을 8분의 단위로 변환 → 8분의 2(²/₈)
- 8분의 2 + 8분의 1 = 8분의 3(³/₈)
✅ 이해 포인트: 통분이 필요한 이유는 ‘단위를 맞추기 위해서’이다.
3. 방정식: x 값을 쉽게 구하는 법
방정식이란?
방정식이란 미지수(x)가 포함된 등식으로, 특정한 값에서만 성립하는 식이다.
※ 예제
✅ 2x + 1 = 5 여기서 x 값을 구하는 방법을 살펴보자.
방정식 풀이법
- +1을 없애려면 양변에서 -1을 빼준다
→ 2x = 4 - x를 구하려면 양변을 2로 나눈다
→ x = 2
✅ 이렇게 한 단계씩 차근차근 정리하면 쉽게 해결된다.
📌 학생들이 흔히 하는 실수
● ‘이항’을 단순 암기해서 무조건 부호를 바꾼다고 생각하는 경우
● 등식의 성질을 활용하지 않고, 그냥 넘기면 부호 바뀌는 거야라고만 알고 있는 경우
✅ 해결법: "넘긴다"는 개념이 아니라 양변에 같은 연산을 적용하는 과정이라고 이해해야 한다.

4. 농도 문제 쉽게 푸는 법
농도란?
농도는 소금의 양이 전체 용액에서 차지하는 비율을 의미한다.
✅ 농도(%) = (소금의 양 / 전체 소금물의 양) × 100
✅ 문제 예제: 17% 소금물 400g에 몇 g의 소금을 넣으면 20% 소금물이 될까?
✅ 풀이 과정
- 400g의 17% = (400 × 17) ÷ 100 = 68g
- xg의 소금을 추가하면 (68 + x) / (400 + x) × 100 = 20%
- 이 식을 정리하면 x = 15g
✅ 이해 포인트: 농도 문제는 공식이 아니라 ‘비율 관계’를 이해해야 풀 수 있다.
📌 학생들이 흔히 하는 실수
● 문제에서 요구하는 게 "추가된 소금의 양"인지, "최종 농도"인지 헷갈림
● 전체 소금물의 양과 소금의 양을 구별하지 않고 식을 세움
✅ 해결법: 문제에서 증가하는 값과 비율을 정확히 파악해야 한다.
5. 정리: 흔한 실수와 해결법
✅ 분수는 나눗셈의 표현이다. 계산법을 외우는 것이 아니라 개념을 이해해야 한다.
✅ 약분과 통분의 원리는 같다. 분모를 곱하는 것이 아니라 공통분모를 찾아야 한다.
✅ 방정식 풀이에서 '이항'은 넘기는 개념이 아니라, 등식의 성질을 이용하는 것이다.
✅ 농도 문제는 단순한 공식이 아니라, 전체 비율을 정확히 이해해야 한다.
마무리 글
수학이 어렵다고 느껴진다면, 문제를 푸는 방법이 아니라 개념을 이해하는 데 집중해 보세요. 정승재 강사의 방식처럼 실생활 예제와 원리를 활용하면 수학이 훨씬 쉬워집니다. 단순 암기가 아닌 논리적인 접근이 중요합니다. 오늘 배운 개념을 다시 한 번 정리하고, 직접 문제를 풀면서 개념을 내 것으로 만들어 보세요. 꾸준히 연습하면 누구나 수학을 잘할 수 있습니다!
'공부지도 > 학습 도움' 카테고리의 다른 글
| AI가 공부법을 추천한다? EBS 'AI 단추 플러스' 무료 이용법 (0) | 2025.03.20 |
|---|---|
| 초등 학습, 언제 어떻게 시작해야 할까? – 일타강사들의 단꿈e 런칭 설명회 핵심 정리 (0) | 2025.03.17 |
| 공부 효율 2배! 성적 급상승하는 7가지 학습 비법 (0) | 2025.03.13 |
| KT, AI 문제풀이 서비스 ‘콴다’ 구독 출시! 무료와 차이는? (0) | 2025.02.24 |
| 이투스247 독학재수학원! 장단점, 비용, 후기 및 경쟁 학원 비교 (0) | 2025.02.10 |




댓글